Canicules reconstruites ! – Blog des méthodes
Message fourni par Loke de Schmalensee
Pendant de nombreuses décennies, les humains ont essayé de comprendre comment traiter les signaux continus pour notre commodité. En conséquence, de nombreuses méthodes innovantes ont été développées pour enregistrer, compresser, restaurer et transformer (et plus) des signaux continus. Considérons, par exemple, la relation entre le traitement du signal et la musique : elle intervient directement via l’enregistrement des ondes sonores, et indirectement via les émissions radio. Malgré l’omniprésence des fluctuations continues et périodiques dans la nature, le potentiel écologique apparemment vaste de la théorie du traitement du signal est resté largement inexploité. Ici, je discute de mon dernier article dans lequel j’introduis deux concepts de traitement du signal écologiquement utiles dans le contexte de l’écologie thermique. Espérons que ce billet de blog offre un angle alternatif, en se concentrant sur la transmission de l’intuition pour pourquoi ces concepts de traitement du signal fonctionnent.
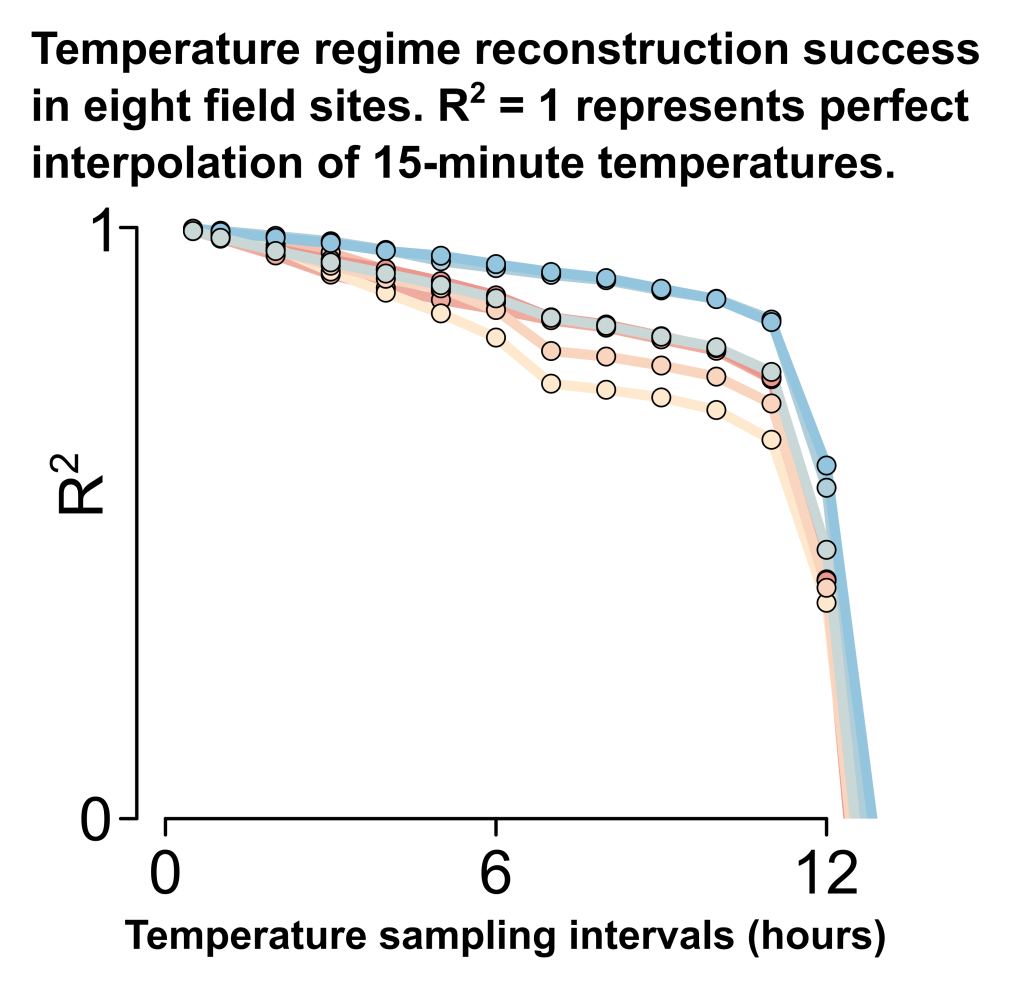
je venais de présenter le premier chapitre de ma thèse de doctorat (au moment où j’écris, je suis encore doctorant) lorsque mon ami qui a assisté à la présentation, Klas Walldén, m’a approché. Il a souligné que l’une de nos conclusions (à savoir, que l’augmentation de la fréquence des mesures du microclimat n’améliorait les prédictions des temps de développement des insectes que lorsque les intervalles de mesure étaient de 12 heures ou moins) lui a rappelé un concept qu’il avait rencontré lors de ses études de physique de l’ingénieur – le « Théorème d’échantillonnage de Nyquist-Shannon“. Bien qu’intrigué, je n’y ai pas beaucoup réfléchi à l’époque, car j’étais préoccupé par d’autres idées. Un an plus tard, le commentaire de Klas a refait surface dans ma mémoire, incitant à une exploration plus approfondie. J’ai appris que, dans les bonnes conditions, des signaux continus pouvaient être reconstruits à partir de mesures étonnamment peu fréquentes (du moins pour moi), et j’ai réalisé que ces techniques d’interpolation pouvaient être appliquées à mes ensembles de données de température microclimatique pour augmenter leur résolution temporelle. Finalement, cela s’est traduit par un article sur l’applicabilité du théorème d’échantillonnage de Nyquist-Shannon et depuis interpolation en écologie thermique. Ici, je décris le contenu de l’article d’un point de vue légèrement différent, partageant les intuitions que j’ai acquises d’une manière qui, je l’espère, est accessible à d’autres écologistes. Mais pour résumer le résultat principal : la plupart des variations de température naturelles dans les séries chronologiques de mesures prises toutes les 15 minutes (c’est-à-dire des données temporellement à haute résolution) pourraient être récupérées de manière cohérente lorsque les températures n’étaient échantillonnées que toutes les 11 heures (voir la figure ci-dessous).
Se déplacer dans les trucs mathématiques
Les références fondamentales de mon article (par exemple, Shannon 1948) sont assez remplis de notation mathématique. En tant qu’écologiste, je n’apprécie pas autant la notation mathématique que les mathématiques. Comme pour les partitions musicales, je peux le lire en théorie, mais cela prendra probablement plus de temps que prévu par l’auteur. En d’autres termes, la notation mathématique est un moyen inefficace de me communiquer des idées mathématiques, et je soupçonne que je ne suis pas le seul parmi les écologistes. Peut-être que privilégier la notation mathématique aux chiffres et au texte brut pourrait même créer des barrières pour les lecteurs écologistes, les amenant à négliger des découvertes pertinentes et importantes (ce qui, ironiquement, pourrait être la raison pour laquelle j’ai pu écrire l’article). Par conséquent, j’utilise ici précisément du texte brut et des chiffres pour élucider certains concepts sous-jacents à mon article, dans le but de les rendre plus accessibles. En échange, je dois m’excuser à l’avance auprès du mathématicien ou de l’ingénieur méticuleux pour la grossièreté de mes explications.
La puissance des séries de Fourier
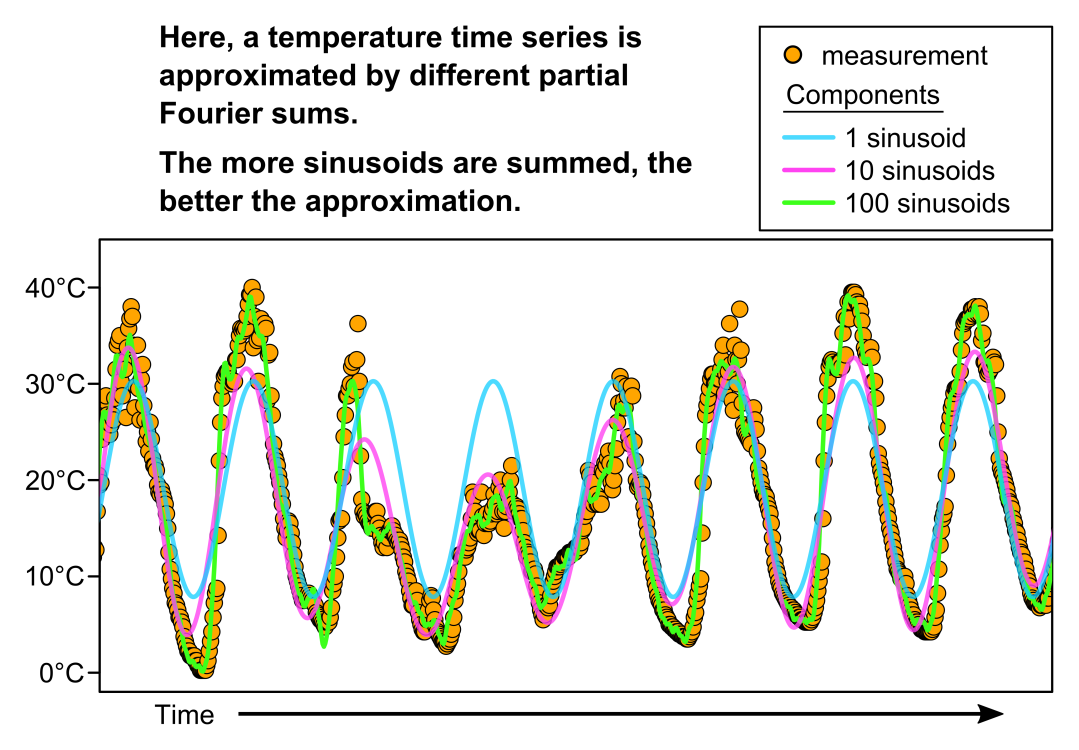
Un acteur clé de cette histoire est le mathématicien Jean-Baptiste Joseph Fourier et sa découverte des séries de Fourier (par coïncidence, il a fait la découverte en travaillant sur la conduction thermique). Fourier a proposé que les fonctions mathématiques puissent être représentées comme des ensembles infinis de sinusoïdes (c’est-à-dire des ondes sinusoïdales et cosinusoïdales), ou « Série de Fourier”. Certes, un autre mathématicien au nom tout aussi long, Johann Peter Gustav Lejeune Dirichlet, a montré plus tard que certaines conditions doivent être remplies pour que cela soit vrai. Néanmoins, une gamme remarquable de fonctions peut au moins localement être bien approchée en additionnant simplement les sinusoïdes, soulignant l’importance de la découverte de Fourier. À partir de là, il est raisonnable de supposer que les régimes de température peuvent également être approximés en additionnant les ondes sinusoïdales et cosinusoïdales. C’est bien le cas, comme le montre la figure ci-dessous.
Comme cela deviendra évident, ce simple fait – que les régimes de température peuvent être décomposés en sinusoïdes séparées (composantes de fréquence) – est fondamental pour l’application de mon article de la théorie du traitement du signal.
Pourquoi les signaux peuvent-ils être reconstruits ?
Dans mon article, j’introduis le théorème d’échantillonnage de Nyquist-Shannon, qui stipule qu’un échantillonnage suffisamment fréquent permet de reconstruire parfaitement des signaux continus à partir de mesures discrètes (par « depuis interpolation » dans le domaine temporel, ou « zero padding » dans le domaine fréquentiel). Je n’écrirai pas ici sur les techniques d’interpolation (pour cela, veuillez consulter l’article). Au lieu de cela, je vais essayer de transmettre mon intuition pour pourquoi un signal continu peut être parfaitement reconstitué à partir de mesures discrètes en explorant un exemple simple : une seule onde sinusoïdale.
Imaginez vouloir reconstruire une onde sinusoïdale inconnue dans une série temporelle composée de mesures régulièrement espacées. Vous commencez par visualiser les mesures (ci-dessous).
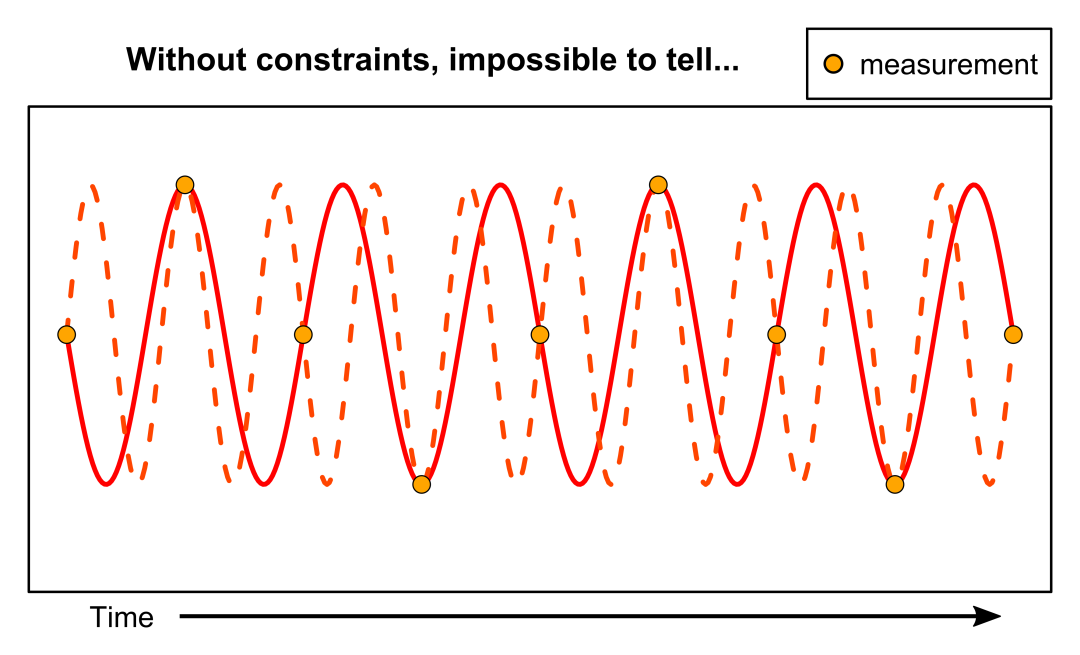
Quelle pourrait être la véritable longueur d’onde de ce signal ? Peut-être que vous reliez les points dans le temps et voyez apparaître une onde triangulaire. Vous pourriez vous dire : « A-ha, une onde sinusoïdale avec les mêmes caractéristiques que cette onde triangulaire correspondrait également aux données. Ça doit être la solution ! » Mais ce serait mal avisé. Sans vous imposer de contrainte sur la fréquence de la sinusoïde que vous recherchez, vous n’avez aucun moyen de trouver une solution. En fait, compte tenu de ces instants de mesure, il existe un nombre infini de fréquences qui généreraient les mêmes données. Voir la figure ci-dessous pour deux exemples.
Le théorème d’échantillonnage de Nyquist-Shannon dit que la reconstruction parfaite d’une sinusoïde peut être obtenue lorsqu’un échantillonnage (périodique) se produit au moins deux fois chaque longueur d’onde. En d’autres termes, les algorithmes d’interpolation fonctionnent sous l’hypothèse qu’aucune composante de fréquence dans le signal échantillonné n’a de longueur d’onde inférieure à deux fois l’intervalle d’échantillonnage (remarque : contrairement à l’exemple de l’onde sinusoïdale unique utilisée ici, un signal peut être une forme d’onde complexe exprimable comme la somme d’un ensemble de sinusoïdes). Sous cette hypothèse, il existe une solution unique à notre question, comme le montre la figure ci-dessous (la ligne noire représente cette solution unique ; les lignes roses représentent les signaux de la figure précédente).
Sur cette figure, il apparaît également que ne pas mesurer le signal assez fréquemment peut entraîner des erreurs substantielles. Imaginez si le vrai signal était en fait la ligne rose continue, pas la noire. Le signal rose donnerait exactement les mêmes mesures que le signal noir lorsqu’il est pris aux points temporels particuliers utilisés ici (comme indiqué par les points orange). Par conséquent, même lorsque le vrai signal est en fait la ligne continue rose, les intervalles de mesure utilisés ici produiront le signal noir dans une reconstruction de forme d’onde. Ce phénomène est connu sous le nom d’aliasing : si le signal est sous-échantillonné selon le théorème d’échantillonnage de Nyquist-Shannon, les ondes à haute fréquence sont interprétées comme des ondes à basse fréquence. Par conséquent, le repliement peut provoquer divers degrés de distorsion dans le signal reconstruit en fonction de l’amplitude relative de la composante haute fréquence sous-échantillonnée.
Il en résulte que pour qu’un signal soit parfaitement reconstitué à partir d’échantillons discrets, il ne doit contenir que des composantes fréquentielles dans une gamme de fréquence limitée ; capturer une onde avec une fréquence infiniment élevée nécessite des intervalles de mesure infinitésimaux, de sorte que le spectre de fréquences doit être limité à une fréquence élevée. Un signal avec une telle borne sur son contenu fréquentiel est dit « limité en bande ».
(Le terme « bande limitée » est resté quelque peu déroutant pour moi. Lorsque j’ai étudié la production musicale, j’ai appris qu’un « filtre passe-bande » filtrerait explicitement les fréquences supérieures et inférieures. Cependant, comme les fréquences physiques ne peuvent pas être négatives, j’ai suppose que l’on pourrait dire que même juste une coupure de fréquence supérieure – un filtre passe-bas – se traduit par un signal à bande limitée, puisque le contenu de fréquence des signaux est nécessairement limité à zéro.)
Pourquoi les signaux peuvent être reconstruits
Nous avons maintenant identifié quelques critères importants sur lesquels repose le théorème d’échantillonnage de Nyquist-Shannon : (1) le signal est échantillonné à des intervalles de temps pairs, (2) le signal peut être décomposé en sinusoïdes distinctes (il y a notre connexion à la série de Fourier !), et (3) le signal est limité en bande. Dans ces conditions, un signal continu peut être parfaitement reconstruit à partir de mesures discrètes (hypothèse de séries temporelles infinies qui peut être ignorée pour la plupart des objectifs écologiques). Cependant, selon le théorème d’échantillonnage de Nyquist-Shannon, cela ne peut généralement être fait que si le signal est mesuré à une fréquence au moins deux fois supérieure à celle de sa composante de fréquence la plus élevée. Mais si la fréquence d’échantillonnage est suffisante et que les autres conditions sont remplies, il n’existe qu’une seule solution au problème d’ajustement d’une sinusoïde complexe à une série temporelle de mesures : le vrai signal !
Qu’en est-il des régimes de température ?
En réalité, les signaux à bande limitée et sans bruit sont difficiles à trouver. Ainsi, l’aliasing se produira, et il existe toute une gamme de techniques ingénieuses conçues pour réduire l’aliasing dans les signaux sous-échantillonnés. Cependant, les spectres de fréquence des séries temporelles de température sont généralement définis par des relations négatives entre l’amplitude et la fréquencece qui signifie que les fluctuations rapides contribuent relativement peu à la variation totale de température (voir aussi l’article et les références qui y figurent). Par conséquent, ne pas saisir ces fluctuations rapides pourrait ne pas entraîner de distorsion significative.
En conclusion, les séries chronologiques de température à résolution relativement faible peuvent capturer les fréquences les plus importantes auxquelles les températures fluctuent. Dans le même temps, des fluctuations plus rapides qui ne sont pas capturées par l’échantillonnage provoquent relativement peu de distorsion (par crénelage) dans le régime de température reconstruit en raison de leurs faibles amplitudes. C’est pourquoi les régimes de température continus peuvent être efficacement reconstruits à partir de données de température temporellement éparses. Pourquoi est-ce important, écologiquement? Eh bien, pour les modèles écologiques, les statistiques sommaires des distributions de température environnementale ne suffisent tout simplement pas…les changements de température ont généralement une signification biologique différente selon les températures auxquelles ils se produisent. Par conséquent, la capacité à générer des régimes de température continus aidera les écologistes à créer des modèles significatifs de réponses dépendant de la température dans la nature.